GEOMETRIA MUNDUAN MURGILDUZ: 2011

DEFINIZIOA

Geometrian, angelua jatorri edo erpin berdina duten bi zuzenerdik, aldeak deiturikoak, osatzen duten irudia da.

Angeluen zabalera gradu sexagesimaletan, radianetan edo gradu ehundarretan neurtzen da.

ADIERAZPENA

Irudi geometrikoetan, angeluak irudiko hiru punturen bitartez adierazten dira. Adibidez, bitez A, B eta C puntuak; erpina A puntuan duen angelua, zuzenerdiak AB eta AC bidez definiturik, bi era hauetara adieraz daiteke:

$\widehat{BAC} \ \ \ \ \ \angle{BAC}$

Angeluaren neurria honela adierazten da:

$\measuredangle{ABC}$

Adierazpen matematikoetan ordea, ohizkoa da angeluak letra grekoen bitartez adieraztea: α, β, γ, θ, ... Letra latindarrak (a,b,c, ...) ere erabiltzen dira.

ANGELUEN NEURKETA

Angelu baten zabalera neurtzeko zuzenerdi batetik bestera biratutako zirkunferentzia-arkutik, zentroa angeluko erpinean izanik, abiatu behar da.
Ondoren, s arkuaren luzera r erradioaz zatitzen da. Emaitza angeluaren neurria izango da radian (rad, labur) izeneko unitatetan. Angelu baterako, arkua marrazteko erradioa aldatzen bada, arkuaren luzera ere proportzioan aldatuko da eta beraz angeluaren neurria konstantea izango da.

Neurri ezberdinetako angeluak, radianetan

Angelua radianetan ez baizik eta beste unitate-sistema batean neurtu nahi bada, $s/r\,$ zatidura $k\,$ berariazko konstante batez biderkatu beharko da.

Sistema hirurogeitarra

Sistema hirurogeitar edo sexagesimalean, zirkunferentzia oso bat inguratzen duen angelua 360 gradu sexagesimaleko neurria du (360° idazten da). Horrela, angeluko arkuak zirkunferentzia osoa hartzen duenean angeluaren neurria 2π radianekoa denez, hiruko erregela sinple batez frogatzen da, sistema hirurogeitarrera aldatzeko $s/r\,$ erlazioari biderkatu beharreko konstantea

$k=\frac{2\pi}{360}$ dela.

Horrela, adibidez $3\pi/2\,$ radianeko angeluaren neurria, sistema hirurogeitarrean, $(\pi/2)\times(360/2\pi)=90\,$ gradukoa da ^[2].

Sistema ehundarra

Sistema ehundarrean, angelu zuzenaren neurria 100 gradu ehundarrekoa (100^g idazten da) da (sistema sexagesimalean 90° da). Zirkulu osoko angelua 400 gradu (400^g) du. Radianak gradu ehundarretara bihurtzeko biderkatu beharreko konstantea $k=\frac{2\pi}{400}$ da.

ANGELU MOTAK

90 gradu hirurogeitarreko (π/2 rad edo 100 gradu ehundar) angeluari angelu zuzen deritzo.
Angelu zuzena baino neurri txikiagoa duten angeluei angelu zorrotz deritze.
180 gradu hirurogeitarreko (π rad edo 200 gradu ehundar) angeluari angelu lau edo angelu lerrokide deritzo.
Angelu zuzenetik angelu laurako bitarteko neurria duten angeluei (90°-180°) angelu kamuts deritze. Angelu osoa zirkulu osoa hartzen duten angelua da (360°, 2π rad edo 400 gradu ehundar).
Angelu nulua 0° edo 0 rad neurria duena da.
Bi zuzenerdik bi angelu sortzen dute: angelu ganbila (edo sarkorra) eta angelu ahurra (edo irtenkorra). Angelu ganbila 180°tik beherakoa da. Angelu ahurra 180°tik gorakoa da.

Angelu motak zabalera edo zabaltasunaren arabera:

Angelu zorrotza: 90 gradutik beherako neurria duena.

Angelu zuzena: Bere aldeak elkarzutak (perpendikularrak) dituen angelua, 90º gradukoa.

�

Angelu kamutsa: 90 gradutik gorako neurria duena.

Angelu laua: 180 graduko neurria duena.

Angelu osoa zirkulu osoa hartzen duen angelua da (360°).

ANGELUEN MUNDURA SARRERA EGITEKO BIDEOA DUZUE HURRENGOA

http://youtu.be/9EZsbSvzdW4

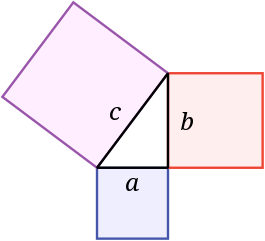
Pitagorasen teorema, ustez, Pitagoras filosofo eta
matematikari greziarrak proposatu zuen, eta honela dio:
"Hiruki zuzen baten katetoen karratua, hipotenusaren karratuaren berdina da."

$a^2 + b^2 = c^2 \,$

FROGAPENA

Demagun triangelu zuzen bat dugula, non a eta b katetoak diren, eta c hipotenusa. c aldearen karratuak osatzen duen azalera, a eta b aldeen karratuen azaleren baturaren berdina dela frogatu nahi da.

c aldearen karratuaren inguruan beste hiru triangelu berdin jartzen baditugu (jatorrizko triangelua karratu horren zentroarekiko 90º jiratuz), karratu berri bat osatzen dugu. Karratu berri honen aldeak a + b neurtuko du, irudian ikusten den bezala.
Karratu honen azalera bi modutan adieraz daiteke: